Maps: 3, Reality: 42 ☺

One of my favorite “trick” questions is “what is the length of the East Coast of the US?” 

First, you may question does it stop at the Texas/Mexico border or the tip of Florida, and what about Key West? A bit more challenging is what about the Chesapeake Bay, and all those rivers? But let’s assume you get past those.

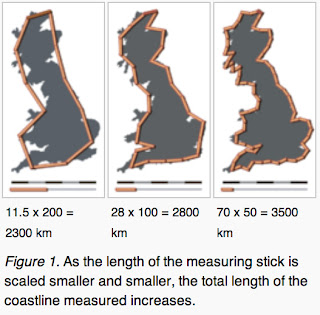
An engineer may just approximate it as 10³ miles, because we are trained to do a quick approximation to test more detailed calculations J. But let’s go with a more experimental approach.

Looking at a map of the whole US and using a 1’ ruler you get one, approximate, length. But using a 1” ruler and you get a longer length. Now go to the individual state maps and do the same exercise: yet longer lengths. What about county maps: longer yet.

Now try walking it, probably better for an armchair experiment, you get longer and longer lengths the shorter your ruler. Consider what length you get if your ruler is a grain of sand. What about a Silicon-Dioxide molecule? …

This is the “Coastline Paradox.” The problem is that coastlines are fractal-like. So the shorter the measure you use, the longer the total length (true fractals have infinite length J). 

This highlights a key difference between constructed items and natural items: constructed regular edges vs. irregular and even changing edges (think about the effect of tides on your coastline measurements). Consider a road vs. a path, a chair vs. a rock, or a swimming pool vs. a pond.

This poses a critical problem for conventional maps, which expect things to be regular and constant (yes they are making progress with traffic, but that is only statistical or sampled). Thus maps do pretty well for roads and buildings (except for example in Death Valley), but not so well for hiking and kayaking (we regularly have to turn back on what the GPS map shows as navigable streams, or even half a lake overgrown with weeds!).

We paddled on a very nice stream, but the topological map of course didn’t show the 7 beaver dams of various heights, but it did show 3 non-existent islands.

So one of the challenges in our new mapping approach is to represent the irregular and changing natures of many of the items we encounter in real life, as opposed to the smooth regular features of artificial constructs, such as roads, although even those are marred by reality, such as pot holes appearing and growing, construction, collisions, and of course traffic.